尾関研究室での取り組み

原子や分子など、多数の要素の集まりが見せる集団での振る舞いを、ミクロな基本原理から導き、理解するのが統計物理学です。物質の性質を基本原理から説明しようとすると、要素数がアボガドロ数（6×10^23）程度になるので、もはや個々の運動を正確に記述することは難しく、また意味もありません。このような体系を集団としてとらえ、マクロな現象を統計的に表現するのです。この作業を厳密に行うことは一般に難しく、これを克服することが統計物理学の担うところです。

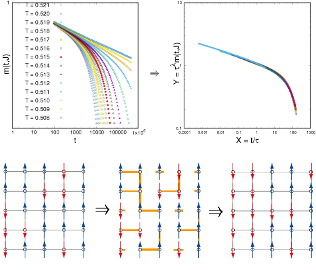
相転移は、アボガドロ数程度の原子・分子が示す典型的な集団現象です。この理解には古くから平均場近似の手法が用いられてきました。平均場近似は現象の本質を捉える良い手法ですが、フラストレーション系やランダム系など、分子間相互作用が複雑な場合には、しばしば適当ではない解を導きます。そのような場合にも適応できる強力な手法の研究や応用が主要な研究テーマです。

非平衡緩和法は、相転移現象を解析できる汎用の数値計算法です。これまでの平衡モンテカルロシミュレーションに比べて、単純で、汎用性が高く、様々な応用が期待されています。